Variance Of Sample Kurtosis

Kurtosis

First we define the sample kurtosis function, as well as a matrix version.

Source: Wikipedia

kurtosis1 <- function(x) {
  xstand <- x - mean(x)
  kurt <- (mean((xstand)^4))/((mean((xstand)^2))^2)
  return(kurt)
}
kurtosis <- function(X) {   apply(X,2,kurtosis1)   }

Generate samples

We select the range of sample sizes and generate a matrix of samples arranged in columns, for each size.

samplesizes <- seq(minsize<-100,maxsize<-10000,stepsize<-50)
nsizes <- length(samplesizes)
nsample.persize <- 500
samples <- vector('list',nsizes)
for (i in 1:nsizes) {
  samples[[i]] <- matrix(rnorm(samplesizes[i]*nsample.persize),samplesizes[i])
}

We used 500 samples of each size ranging from 100 to 10000 in steps of 50.

Calculate Kurtosis

We use parallel processing to speed up the computation. Set cluster size to number of available cores.

library(parallel)
cl <- makeCluster(4)
nul <- clusterExport(cl,c('kurtosis1','kurtosis'))
system.time({
outputs <- parLapply(cl,samples,kurtosis)
})

##    user  system elapsed 
##    4.83   12.77   37.06

stopCluster(cl)

Variances

We calculate the variance for each sample size and do a regression on the results.

vars <- unlist(lapply(outputs,var))
lvars <- log(vars); logn <- log(samplesizes)
summary(m1 <- lm(lvars~logn))

## 
## Call:
## lm(formula = lvars ~ logn)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.180953 -0.043097  0.003116  0.044296  0.166688 
## 
## Coefficients:
##              Estimate Std. Error t value            Pr(>|t|)    
## (Intercept)  3.141518   0.042761   73.47 <0.0000000000000002 ***
## logn        -0.996792   0.005152 -193.46 <0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.06569 on 197 degrees of freedom
## Multiple R-squared:  0.9948, Adjusted R-squared:  0.9947 
## F-statistic: 3.743e+04 on 1 and 197 DF,  p-value: < 0.00000000000000022

b0 <- exp(coef(m1)[1])
plot(samplesizes,vars,type='l',log='xy')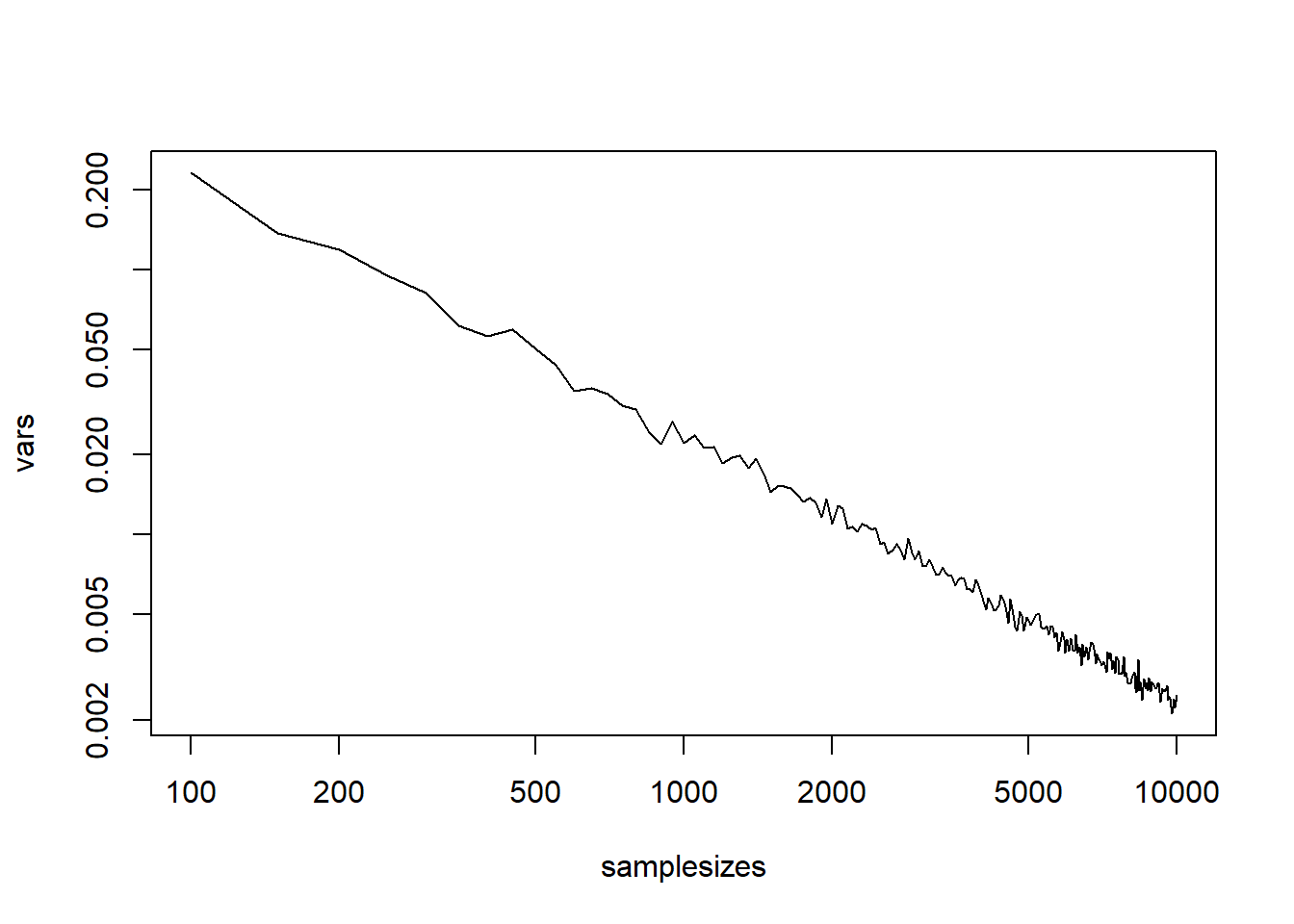

The regression seems good.

Conclusion

The final estimated formula is \(v\approx\) 23.1389604 \(n^{-0.9967917}\).

Thus it is clear that the formula suggested on Wikipedia is correct.

That is \(v\approx \frac{24n(n-1)^2}{(n-3)(n-2)(n+3)(n+5)}\).