The Power of R Markdown for Assessment and Teaching

Sean van der Merwe

Introduction

Motivation

• I am grateful for the opportunity to learn from everyone.
• I am grateful for the tools I have found that enable me to do better.
• I am grateful to be able to share what I have learned with you.

Short abstract

• Student copying in assignments and quizzes can be dramatically reduced, without extra strain on lecturers.
• Sounds too good to be true, but I have done it successfully.
• Once copying is no longer a stressor, the knock-on effects are extensive:
  • Not only are assessments more valid,
  • but deep learning and acquisition of graduate attributes appear drastically increased.
• The key is the use of cutting edge open-source tools, primarily R Markdown and R exams, to create randomised assessments.

Overview (refresh if not showing)

Assessment must keep up with the times

• My professors had no interest in preparing students for the workplace
  • They wanted to make new versions of themselves
  • The temptation to do the same with our students is an ever-present danger
• The workplace requires new skills (Dolezel and McLeod 2021)
• Mathematical statistics students need to be able to
  • use statistics, coding, mathematics, and general research skills
  • to solve real problems related to data (Radovilsky et al. 2018)
  • and present the solutions in clear and practical terms
    • to non-statisticians (Demchenko et al. 2019)

New thinking is needed

• There are things to memorise
  • But it is theory, not theorems
• There are things to understand
  • But it is assumptions and their impact, not weird squiggles
• There are things to apply
  • But we can’t just apply textbook methods to textbook examples, not when the textbook methods only work on the textbook examples
• There are things to analyse
  • But every analysis is unique, not just a set of steps to follow

New thinking is essential

• We need to evaluate all the skills our students will require
• And create new ways to learn, teach, and assess those skills

But we are not alone, the whole world faces these problems, and we don’t need to each solve all the world’s problems. We can learn from each other, like we are doing today 😀

• I’m lazy, but I also like getting things done, so I’m all about efficiency
• But efficiency is not productive without an effective goal:
  • My goal has always been deep learning via valid assessment
  • See my teaching philosophy at https://seanvdm.co.za/project/teaching

Efficiency requires tools

• Civilisations that used the tools of metalworking generally prospered over those who did not, and the tools of industrialisation revolutionised our way of life; similarly,
• Those who can use the tools of the information age can make an impact that changes the face of our industry
• I have not invented new tools but I have mastered some that are hot off the forge and already shifting paradigms in a big way
• My goal is to show you a unified set of tools invented by programmers, statisticians, and others, working together to make everyone’s lives easier
• And I will show that these tools are useful in every field, not just mine

Randomised Assessment

Short version

• I set an assessment once,
  • but the assessment each student sees is different
  • The same outcomes are assessed,
  • but random differences are present in the inputs
• Students are forced to collaborate positively
  • As they would in the workplace
  • Not just copy each other
• I create one memo and one rubric, but
  • The memo each student sees is different, unique to them
• Almost no extra work, just increasingly valid assessments

Like question pools but better

• We know question pools help, and have known for a while (Blanco and Ginovart 2012)
• We also know that question pools can be fair and valid assessments (Fowler et al. 2022)
• But the more aggressively students want to cheat the more effort is required to thwart them (Murdock, Brenneman, et al. 2020), with large classes requiring very large pools of questions for each assessment
• What if you could generate pools of thousands of questions in a day? How would that impact your workflow?

Impact

• Copying becomes so obvious and easily penalised that students don’t even bother trying it
• My tests are open internet access with minimal invigilation needed
  • I can promote graduate attributes in every assessment
• Group work becomes organic and natural
  • I don’t need to check that each person contributes because each person has to apply what the group has learned and draw their own conclusions
• Disruptions aren’t disruptive (no standards were compromised during lockdown or protests)

Side effects

Because I’m no longer so worried about copying and trying to thwart dodgy students …

• I am free to put my creativity towards engagement and deep learning activities
• I don’t need to assess the same thing in as many different ways
  • Instead I can tailor assessments to outcomes
    • I use many different types of assessment in my course, including tests, assignments, quizzes, essay, discussions, interviews, presentations, engagement awards, portfolio, …
• No shortcut to marks: Students make a clear choice between deep learning or losing out on marks
  • A lot of students do choose the second option, but at least the marks I award are authentic

Appreciation

• Students take a while to appreciate what I’m trying to do
• The big shift happens when students start to work
  • I have gotten students contacting me from their workplace saying how useful the skills are that they picked up in my course(s)

Hi Sean, I just wanted to thank you for the exciting things I learned in Bayesian Analysis during the first semester. I was particularly happy about the practical way in which you introduced us to Stan 🙂 and writing a test / presenting something every week also kept me on my toes. The course finally unlocked the fun ways of Bayesian analysis for me and I am happy that I can now apply this to my own research. Thanks again! Sincerely, Trudie

Delayed feedback

Before using these approaches all feedback received focussed on technical aspects of the courses, things like number of assessments, feedback approaches, workload, “number the pages in the notes” 😉. Little was related to what they actually learned.

After making the changes not only did the feedback change in the direction of course outcomes and skills, but there was an increase in delayed feedback - indicating a more lasting impact (and deep learning).

The module was interesting, and I believe that most of its basics will help me in my future research. It had too much of complicated R programming, however i believe i have fallen in love it, since i have noticed that it is currently being used in most contemporary fields that are taking over the world, such as data-analytics, big-data and data-Science. Thanks again for helping me in climbing the academic ladder … Stanley Lekata

Markdown and notebooks

One tool for everything

• Markdown is an idea that simplifies document preparation
• It boils down to programming a document by typing what you mean
  • You type hashes to start headings, stars for formatting, …
  • You can integrate text, formulas, code and results all in one, no copy-paste needed
• I use it for teaching, assessment, research, consultation, websites, and presentations 😉
• The specific platform I use is R Markdown, powered by the open-source language R (R Core Team 2022)
• The idea of literate programming has been around for decades (Lamport 1991), but R Markdown flips the concept by integrating the document preparation into the development environment

Assessment examples

Simple example: averages

• In this question we just generate a few random numbers and ask the students to calculate the average.
• The question presented to the students is just:
  • “What is the average of the numbers 70, 67, 56, 23, 31?”
  • Except that every student gets their own numbers.
  • The solution section is optional, but it is nice to give feedback.

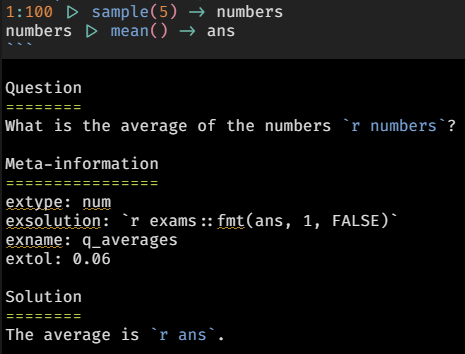
• This is inspired by the ‘calculated’ question option that started with WebCT (which I used in 2006 already) but is way more powerful because it leverages R, via the new package R/exams.

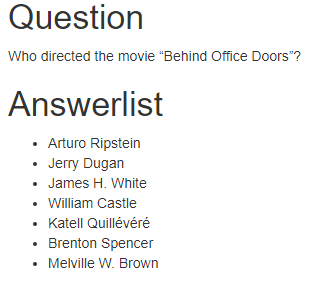
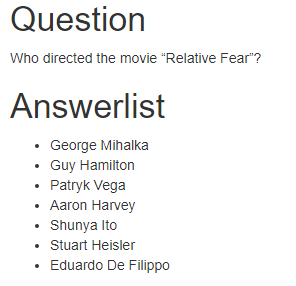
Example: Quiz question pool

• Suppose you want to test students’ internet search skills.
• You could ask a question like the one on the right:
• But now the first student looks it up and shares with the rest, defeating the purpose.
• One solution is to have each student get a different movie and options.
  • If you have 1000 students you need 1000+ questions, manually doing this is not an option.
  • Instead we program the question, picking a movie, the correct director, and a bunch of wrong directors at random.

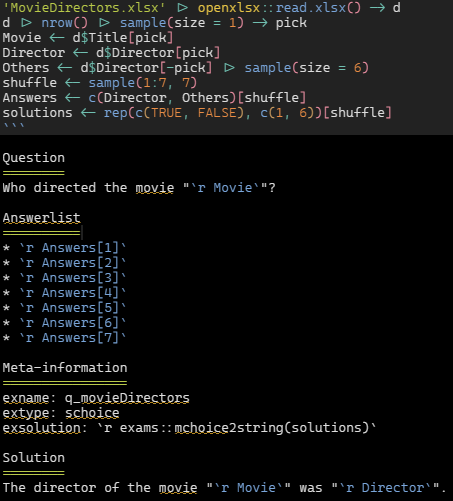
Example: Quiz question pool code

• I created an Excel sheet with lots of movies and directors from the internet.
• I then write a little block of code that picks one at random, getting the title and director.
• I then pick 6 random directors from the rest. I shuffle the 7 directors, remembering which one is the correct one.
• I type the question itself, putting easy code in key places in the question text.
• The final step is to request say 1000 different copies, nicely zipped up for easy upload to Blackboard.

exams::exams2qti21("q_movieDirectors.Rmd", n = 1000, name = "MovieDirector", points = 5)

Random fun with plots

Because we now have the power of R available we can do just about anything.

• We can have questions with random plots:

“Which one of the following four time series is most likely to be stationary?”

Random fun with maths

“Let \(X\) be a random variable on the domain 0 to 1, with density function \(f(x) = 1.5 (x^2 + 2/3 x)\). What is the \(P[X> 0.3]\)? [Accurate to 3 decimals]”

Solution:

\(F(x)=1.5\int_0^x u^2 + 2/3u = 1.5\left[\frac{1}{3} u^3 + \frac{2/3}{2} u^2\right]_0^x = 1.5\frac{2x^3 + 3*2/3*x^2}{6}\)

\(P[X>0.3] = F(1) - F(0.3) \approx 0.9415\)

“Let \(X\) be a random variable on the domain 0 to 1, with density function \(f(x) = 2 (x^2 + 1/3 x)\). What is the \(P[X> 0.5]\)? [Accurate to 3 decimals]”

Solution:

\(F(x)=2\int_0^x u^2 + 1/3u = 2\left[\frac{1}{3} u^3 + \frac{1/3}{2} u^2\right]_0^x = 2\frac{2x^3 + 3*1/3*x^2}{6}\)

\(P[X>0.5] = F(1) - F(0.5) \approx 0.8333333\)

Larger assignments

• For assignments I generate random data for each student (with the same structure) and put it in an Excel file with a sheet named after every student.
  • Using a few lines of R code, I don’t actually need to open Excel at all.
• I then create a memo with questions and answers based on the data of one student, in RStudio.
• When I click a button it asks for the student number and generates the memo for that specific student, as a Word document or PDF.
• So I can give the students (and markers) one file from which each can get their own personal memo.
  • Or I can write a few more lines of code that generates each student’s memo and emails it to them individually.

Teaching

Interactive classes with instant notes

• In dynamic classes fresh topics will come up, thus
• I sometimes create examples on the fly using interactive tools, typing explanations, maths and code between each other, with links to sources.
• At the end of the class I click a button and get a PDF summary of the class to post on Blackboard.
• For example, to teach multivariate simulation I found the following line of code on a website and used the graph to teach some concepts live:

plotly::plot_ly(z=~volcano) |> plotly::add_surface()

Conclusion

The end

Thank you for your time and attention.

I really hope I could inspire some people, or at least broaden minds as to what is possible.

Yes, new tools have a learning curve and require some creativity to implement at first, but the long run efficiency is worth it.

References

Blanco, Mónica, and Marta Ginovart. 2012. “On How Moodle Quizzes Can Contribute to the Formative e-Assessment of First-Year Engineering Students in Mathematics Courses.” RUSC, Universities and Knowledge Society Journal 9 (1): 354–70.

Demchenko, Yuri, Tomasz Wiktorski, Juan Cuadrado Gallego, and Steve Brewer. 2019. “EDISON Data Science Framework (EDSF) Extension to Address Transversal Skills Required by Emerging Industry 4.0 Transformation.” In 2019 15th International Conference on eScience (eScience), 553–59. https://doi.org/10.1109/eScience.2019.00076.

Dolezel, Diane, and Alexander McLeod. 2021. “Big-Data Skills: Bridging the Data Science Theory-Practice Gap in Healthcare.” Perspectives in Health Information Management 18 (Winter).

Fowler, Max, David H Smith IV, Chinedu Emeka, Matthew West, and Craig Zilles. 2022. “Are We Fair? Quantifying Score Impacts of Computer Science Exams with Randomized Question Pools.” In Proceedings of the 53rd ACM Technical Symposium on Computer Science Education v. 1, 647–53.

Lamport, Leslie. 1991. LaTeX. ŚCompany Cyfronet.

Murdock, Mark, Matthew Brenneman, et al. 2020. “DESIGNING TESTS FROM QUESTION POOLS WITH EFFICIENCY, RELIABILITY, AND INTEGRITY.” Journal of Contemporary Chiropractic 3 (1): 92–100.

R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Radovilsky, Zinovy, Vishwanath Hegde, Anuja Acharya, and Uma Uma. 2018. “Skills Requirements of Business Data Analytics and Data Science Jobs: A Comparative Analysis.” Journal of Supply Chain and Operations Management 16 (1): 82–101.

Other things (for interest)

Survey reports

• I’ve had to analyse surveys with hundreds of questions.
• Clients need reports that have tables, plots and other summaries.
  • Of course the reports must still be easy to navigate and in a format they are used to, usually Word.
• Since the Word document is created by processing ordinary text, that text can be meta-programmed.
• So a report of hundreds of pages can be created by a bit of code that fits on one page.
• The best part is when the client sends updated data and I can produce a new report in seconds.

Interactive presentations

• The most fun part is creating interactive content.
• My website was created in RStudio.
• This presentation was created in Quarto in RStudio.
  • Quarto allows you to use R, Python, Julia, LateX, Javascript, HTML, and similar stuff in the same document!
  • You type your content once, then go from rendering HTML to PowerPoint to PDF with a single step.
    • The power comes from typing what you mean and letting the tools do the hard work of actually making a presentation.

Module evaluation system

I created a new module evaluation system for my faculty by leveraging some new tools.

• I created a report framework with all the text, headings, links, and structure that is common in all cases.
• I then include R code that processes the survey data of a specific module plus lecturer.
  • The code produces summaries, plots, tables, and so on.
  • R is unquestionably the best tool for this process, by far.
  • I can then click a button to get a Word report for a module.
• I take it a step further: I write another block of R code that compiles the report for module after module in a loop, each time telling R to process the report as if I was pressing the button and telling it who the lecturer is (and module code).