November 2020
Session 1 Part 1
Arrangements
- Even number of people in each row please. Every two people will be a team so make sure you can get along with the other person in your pair.
- Please keep your mask on and don’t sit right next to each other.
- Pen and paper will be handy for taking notes.
- There will be a single break in the middle of each session.
- Everyone is required to follow along and to take part actively.
- What you do and get on your computer will not and should not match what is on my slides. I have purposefully introduced differences between my code and results to stimulate conversation.
- Also feel free to ask about your error messages.
Isses and isn’ts
- This course is not:
- Serious
- Counting towards anything
- Official
- Formal
- Intense
- So please avoid using swearwords like ‘work’ or ‘responsibility’ in these sessions.
- This course hopefully is:
- Interesting
- Fun
Why R?
- Freedom.
- With R you can do what you like without worrying about the limitations of the software.
- The only limitation is you:
- The more open you are to trying things the more you will learn.
- The more you open your mind to learning better approaches the more interesting you will find even the simple things.
- So don’t just try to solve the problem, try to solve yourself 🙂
Example from another field
- A survey was done on the use of ‘Oom’ and ‘Tannie’ among Afrikaans speakers.
- I was asked to do the superficial analysis of the responses, including tables, graphs, and statistical tests comparing responses to various questions. I produced a 150 page report containing all the requested results.
- When presenting the results I asked why non-Afrikaans speakers were included in the data. I was told that this was a mistake and that the data should be filtered for only Afrikaans speakers.
- So how long do you think it took me to filter the data and produce a new 150 page report? Write down your guess and then we see who gets closest.
What is R?
- R is just an interpreter for doing things with data
- An interpreter runs commands one block at a time before moving on to the next one
- It does not compile things into programs that run on their own, R programs need R to run
- Other interpreters you might have heard of include Logo and Basic (including VBA)
- At its core R lets you type, paste, or read in commands in plain text and then spits out more text and basic graphs
- However, R is so much more than its core for a few reasons:
- R is infinitely extensible — you can make it grow and expand to suit your needs
- The core is small, solid and well designed, so easy to get and install. This makes more people willing to try it
- Because millions of people were willing to try it, and a good portion of those were willing to expand it, it has grown to be amazingly powerful
Options
UFS staff (and to a lesser extent students) are privileged to have access to many premier statistical packages.
The biggest, and probably best, is SAS. Base SAS is a scripting language, like R, although with a vastly different syntax. On campus we also have the fantastic interfaces for it, like Enterprise Guide and the data science interfaces.
If you are doing standard statistics on well organised data and want robust trusted results then consider using SAS Enterprise Guide. It is installed on the computers in the teaching labs, so I recommend you go there and run what you need to. I do not recommend getting it on your computer though, not without good reason. Be sure it works for you before you get it for yourself.
Other options include Mathematica, Stata, Statistica, Matlab, and specialised programs for your field.
I have used all of the packages on this slide at some point. Now I only use R for all my work.
Getting help
LinkedIn Learning is the official UFS platform for learning things and it has a lot of stuff on R. Much of it is likely to be better than what I’m doing.
The Help menu in RStudio has a ton of useful links to various sources of help and inspiration.
If you click in the Console window and type ? followed by the command you want help with then it will tell you tons about that command. If you almost know the command then type ?? instead.
Try it now, open RStudio if you haven’t yet, click in the console window, and type ?library
Packages
- The true power of R comes from the way that thousands of people contribute to making R better.
- Since they do it for free, it is only right to credit them.
- Always cite at least base R in your publications if you use it.
- You can also cite specific packages that you found helpful.
citation()
##
## To cite R in publications use:
##
## R Core Team (2020). R: A language and environment for statistical
## computing. R Foundation for Statistical Computing, Vienna, Austria.
## URL https://www.R-project.org/.
##
## A BibTeX entry for LaTeX users is
##
## @Manual{,
## title = {R: A Language and Environment for Statistical Computing},
## author = {{R Core Team}},
## organization = {R Foundation for Statistical Computing},
## address = {Vienna, Austria},
## year = {2020},
## url = {https://www.R-project.org/},
## }
##
## We have invested a lot of time and effort in creating R, please cite it
## when using it for data analysis. See also 'citation("pkgname")' for
## citing R packages.
Rmarkdown interface
I use Rmarkdown for almost everything, including teaching, assessment, consultation, some research, and even making presentations like this one.
To use Rmarkdown you open RStudio, click File -> New File -> R Markdown…
To put in code you click on the Insert button at the top right of the code window, then click R. Type some code in the block, say sqrt(5).
Everything else is part of the text. Markdown mixes text, code, and output neatly in one document. Click on Knit to make a document now.
Classic example: Fisher’s Iris data
Type these commands and press Ctrl+Enter at the end of each line to run it, or use the play button in the top right corner of the block to run the whole block.
# The hash in R is for typing comments, you only need to
# type what's before the hash
data(iris) # R has a lot of example data sets built in, this loads one of them
summary(iris) # The summary command makes a summary of data or model output
View(iris) # For viewing data in RStudio, same as double clicking on data in Environment
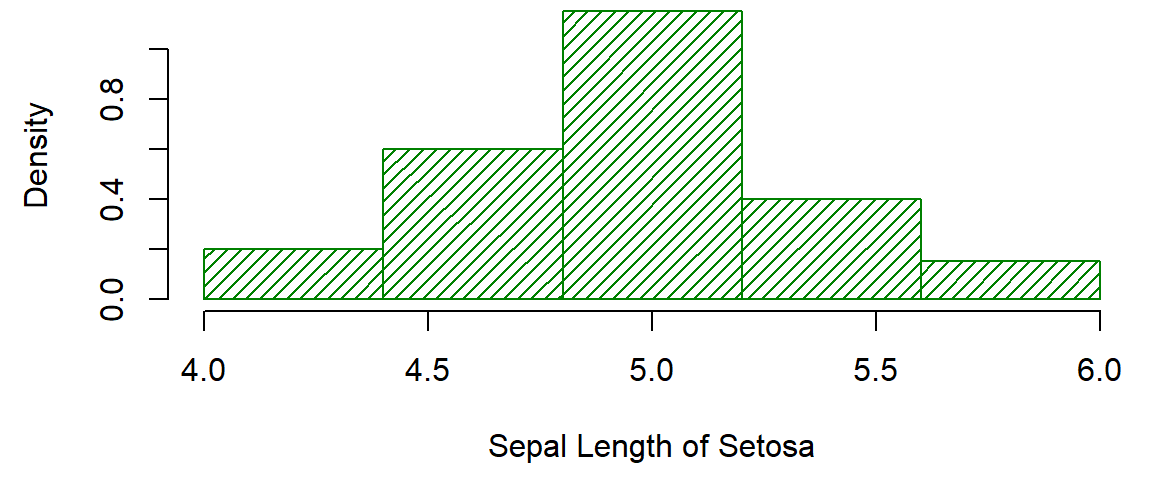
hist(iris$Sepal.Length[iris$Species == "setosa"], 8, col = "purple",
xlab = "Sepal Length of Setosa", main = "") # Histogram
You must enable Javascript to view this page properly.
Try for yourself 1
Make your histogram:
- Have relative frequencies on the y-axis (density)
- Not solid, striped fill instead
- Be your favourite colour
- Have bars from 4 to 4.4, 4.4 to 4.8, 4.8 to 5.2, 5.2 to 5.6, and 5.6 to 6
Session 1 Part 2
Principle Components Analysis
PCA is used to reduce the number of variables in a block of data, by creating orthogonal linear combinations of the variables, while keeping the amount of variation retained as large as possible for linear combinations. Try the following:
myPCA <- prcomp(iris[, 1:4]) summary(myPCA) plot(myPCA, type = "l")
| ItemNumber | Item | PC1 | PC2 | PC3 |
|---|---|---|---|---|
| 1 | Standard deviation | 2.056 | 0.493 | 0.280 |
| 2 | Proportion of Variance | 0.925 | 0.053 | 0.017 |
| 3 | Cumulative Proportion | 0.925 | 0.978 | 0.995 |
Iris PCA results
The Iris PCA said that we only need 1 dimension to capture 92% of the variation in the measurements. However, this is an unsupervised learning method, meaning we haven’t looked at the target variable — species — at all yet.
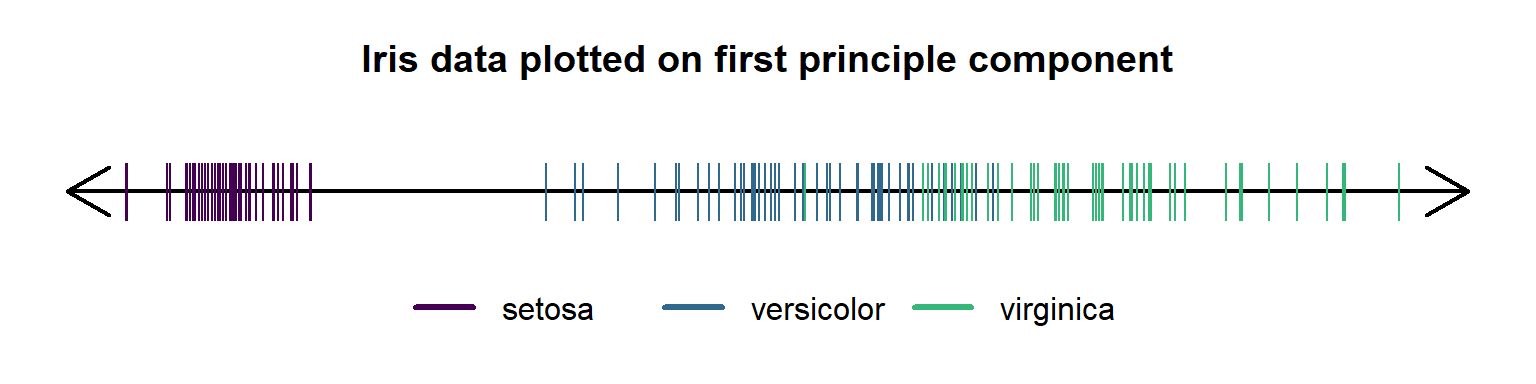
We can see that it did not separate the species because that’s not the point of PCA.
Loading data from Excel
To load data from Excel files we first load the openxlsx package.
library(openxlsx)
mydata <- read.xlsx("nitrogen.xlsx", "Export")
If the package is not installed yet, then you will need to install it first, by running this command in the Console:
install.packages("openxlsx")
Remember that you install a package only once, using the console, and from then on you just load it every time you need it (by putting the library command near the start of your program that needs it).
Data loading practice
Test yourself:
- Make sure the nitrogen data is read into the mydata variable and give a summary of the data.
- Also read in the info sheet and View it.
- Calculate the standard deviation of Initial_NH4plus.
- Draw a histogram of N_Balance.
Homework
For the next session everyone must bring along a paper with some statistics.
At random times a person will be asked to explain to everyone what statistics was done in the paper they brought and why they think it was done that way.
Most of Session 2 and 3 will focus on statistical modelling.
- Linear models
- ANOVAs
- GLMs
- Mixed models
- Exotic models
Session 2
Recap
What was the most common mistake in R you’ve made so far?
What was the first thing that you forgot from Session 1? What was the most important thing you forgot and wish you could remember?
How to relearn the things you forgot:
- Google first, ask questions second
- Use RStudio help window search box
- Look for a guide on the internet, like https://www.tutorialspoint.com/r/index.htm
Without looking
- Make a new R Markdown document for this session.
- Clean it up by removing the stuff after the setup chunk.
- Save it in the same place as the nitrogen data.
- Make a new code block.
- Load the nitrogen data and store it in a variable called mydata.
- Make another new code block.
Vectors
Let’s take a detour quickly and talk about vectors.
In R we put numbers together using c(). This is the concatenate function and creates a vector.
- It will automatically take on the simplest type that can handle everything you put in it.
- If all the numbers are integers then you get an integer vector, e.g. c(4,5,6) is 4 5 6
- If some of the numbers are real then they all become real, e.g. c(1.2,3,4) is 1.2 3.0 4.0
- If you include text then the whole vector becomes text, e.g. c(1,2,‘see’) is ‘1’ ‘2’ ‘see’
Sequences
There are lots of ways to make sequences. We’ve already see the colon notation for integer sequences, but try a few more:
3:8 7:2
You can make more complicated sequences using the seq command:
seq(10, 40, 5) seq(10, 100, length = 10)
But the most fun way to make sequences is with the rep command:
rep(c(2, 4, 7), each = 2, times = 3) rep(c(1, 2, 3), c(3, 4, 5))
Box plot
A histogram does not let us see what is happening with the different treatments, but a box plot might.
boxplot(mydata$N_Balance ~ mydata$Treatment)
par(mar = c(4.5, 4.5, 0.5, 0.5))
boxplot(mydata$N_Balance ~ mydata$Treatment, col = 2:7,
xlab = "Treatment", ylab = "Nitrogen Balance")

Data Frames
The rest of this session will be devoted to working with data frames. A data frame is also a matrix and a list of variables. This means that there are tons of ways of working with a data frame.
- Matrix form: You can refer to cells using row and column numbers in single square brackets
- It’s dataframename[row number(s), column numbers()]
- So mydata[1:5, 1:2] means the first 5 rows of the first two columns
- Leaving rows blank means all the rows, e.g. mydata[,3] means the third column
Data Frames as lists of variables
- Use $ and start typing the variable name, then tab to auto-complete
- Use double square brackets with the number of the variable
- You can use single square brackets to get sets of variables, e.g. mydata[1:2] returns the first two columns
- You can also attach a data frame to extract all the columns into separate variables with their own names
- If you’re only going to work with one set of data and all the columns have neat and easy to type names that don’t conflict with your code then this is a good idea
- If your data is changing or you’re importing multiple data sets then this is a bad idea because it’s easy to get confused
Test yourself
What’s the difference between using double and single square brackets?
Hint: use the class function to find out. The class function is extremely important when learning R in order to debug a lot of things going wrong.
Try to use a command to get the variables that start with ‘Delta’.
Hint: use the names function inside the startsWith function in the square brackets.
t tests
Let’s do some t tests. First we will do paired tests:
t.test(mydata$Delta_NH4plus, mydata$Delta_NO3minus, paired = TRUE) t.test(mydata$Delta_NH4plus - mydata$Delta_NO3minus)
Then let’s make a factor that’s High when N_Balance is more than 15 and Low otherwise and do a two sample test:
NBhigh <- mydata$N_Balance > 15
t.test(mydata$Delta_NH4plus ~ NBhigh)
t.test(mydata$Delta_NH4plus[NBhigh == 0], mydata$Delta_NH4plus[NBhigh ==
1])
# Alternatively:
NBhigh <- factor(mydata$N_Balance > 15)
levels(NBhigh) <- c("Low", "High")
t.test(mydata$Delta_NH4plus ~ NBhigh)
Other simple hypothesis tests
The t test assumes something roughly resembling normality (bell shape). It is robust to small violations, but not severe violations. For example, a t test works for Likert scale data that is not too far to one side or the other, but not for data that has extreme values or outliers.
You can test for normality using shapiro.test but a histogram is generally better.
If you want to use a non-parametric alternative you could try wilcox.test. It still tests location, but not the mean (average) like the t test. It is a safer test, but not as powerful.
`?`(shapiro.test) `?`(wilcox.test)
Session 2 Part 2
Modelling
Statistical modelling is my favourite topic.
We will start with linear models and ANOVAs.
To do an ANOVA you always first do a linear model with the factors listed as explanatory variables in order of importance.
Regressing numbers on text doesn’t make sense, the text factors must be turned into numbers first. However, R does this automatically for you, and does it better than I would. It correctly makes binary (0,1) dummy variables for each category after the first (base) category for each factor.
Linear model notation
Models are specified using a special syntax inside the command `lm’:
- ‘\(\sim\)’ separates the dependent variable on the left of it with the model on the right of it.
- ‘+’ adds a variable to the model
- ‘.’ indicates all the available variables (requires specifying a dataset)
- ‘1’ refers to a constant/intercept (column of ones)
- ‘-’ excludes a variable. For example, the intercept is automatically included in every model, so to exclude it use ‘-1’.
- ‘:’ between two variables indicates the interaction
- ’*’ includes both variables and their interaction
Implementation
Let’s run a model and store the fit:
model1 <- lm(mydata$N_Balance ~ mydata$Treatment) # OR model1 <- lm(N_Balance ~ Treatment, data = mydata) # Then summary(model1)
- Use summary to get nice output
- Use plot for some diagnostic plots
- Use residuals or resid to get the residuals for testing, e.g. shapiro.test(resid(model1))
ANOVA
An ANOVA table is calculated from a linear model fit by applying the anova function:
anova(model1)
## Analysis of Variance Table ## ## Response: N_Balance ## Df Sum Sq Mean Sq F value Pr(>F) ## Treatment 5 149.077 29.8155 14.704 0.0001489 *** ## Residuals 11 22.305 2.0277 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Application
Now we will load a new data set and apply the stuff we learned today.
So start a new R Markdown file, clean it up, and save it.
Download the file GlutenDatasetforR.xlsx and put it in the same folder. Note that I have not modified this file in any way from when I received it.
Normally there is a lot of work to do before we use the data, which is often easier to do in Excel; but this sheet is well constructed and nearly ready for use, so in this case we will fix it in R for extra learning.
So please load the data into R in a variable called gluten.
View and edit
View the data in RStudio.
Note that we can’t modify data directly in the viewing window, we have to use code, unlike Excel. However, code is systematic, clean, and repeatable, which is a requirement in some cases.
We can see that every second repetition of “ATILC 2000” has a space in the middle that needs to be removed. Try to fix this now.
Hint: Either search for Name == “ATILC 2000” or for the joint case of Entry == 4 and Rep == 2.
Edit 1 result
You will know you have done the edit correctly if you run this command and get the result given below:
levels(factor(gluten$Name))
## [1] "ALTAR84" "ATILC2000" "CIRNOC2008" "JUPAREC2001" "MEXICALIC75" ## [6] "YAVAROS79"
What is the difference between the above command and unique(gluten$Name)?
Factors
If we tell R to use Treatment as an explanatory variable then R will turn it into a factor because it is stored as text.
unique(gluten$Treatment)
## [1] "Control" "Drght" "Flood" "Heat" "MeDS" "MeHS"
If we put this into a regression then for every level of the factor except the first (every treatment) R will create a variable that is 1 for that treatment and 0 for every other treatment.
The interpretation of the regression coefficients are then relative to the base treatment.
Numeric factors
Year is not stored as text, so R thinks it is just numbers. If we put it in a regression then it will consider 2014 as being two 2013s because it is saved as 2 versus 1.
Since their are only two levels for Year in this data we could subtract 1 so that we have 1 versus 0 directly. This will not work right if their are more than two years.
The general solution though is to tell R explicitly that Year is a factor:
gluten$YearFactor <- factor(gluten$Year)
levels(gluten$YearFactor) <- c("2013", "2014")
ANOVA 1
We can now do the ANOVAs. To start with we use Treatment, YearFactor, and Name as main effects without interaction. We will use the first measurement first.
anova(glutenM1 <- lm(LUPP ~ Treatment + YearFactor + Name,
data = gluten))
## Analysis of Variance Table ## ## Response: LUPP ## Df Sum Sq Mean Sq F value Pr(>F) ## Treatment 5 2030.8 406.16 5.3546 0.0001629 *** ## YearFactor 1 1286.5 1286.46 16.9601 0.00006692 *** ## Name 5 326.1 65.23 0.8599 0.5100278 ## Residuals 132 10012.5 75.85 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
ANOVA 1
We can adjust the model and compare information criterion values to find the most parsimonious model:
anova(glutenM2 <- lm(LUPP ~ Treatment * YearFactor, data = gluten)) anova(glutenM3 <- lm(LUPP ~ Treatment + YearFactor, data = gluten)) AIC(glutenM1, glutenM2, glutenM3) BIC(glutenM1, glutenM2, glutenM3)
| df | AIC | BIC | |
|---|---|---|---|
| glutenM1 | 13 | 1045.471 | 1084.078 |
| glutenM2 | 13 | 1039.183 | 1077.791 |
| glutenM3 | 8 | 1040.086 | 1063.845 |
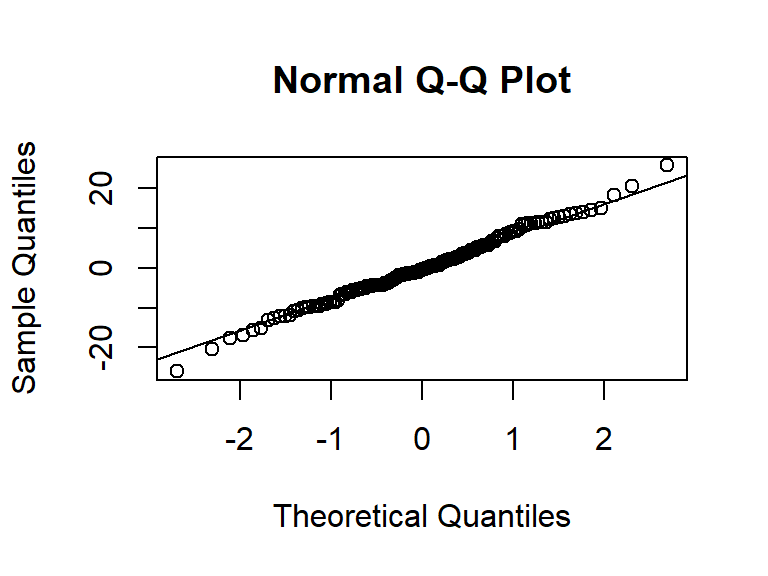
Residuals
Let’s test the residuals for normality:
r1 <- resid(glutenM3) shapiro.test(r1) qqnorm(r1) qqline(r1)
Homework
Next time we will see ways to efficiently do the above analysis for all the measurements (not just one at a time).
For now though, manually do the analysis for the FP_14 variable.
Also, try to make notes about what you understood and didn’t understand.
Bonus fake points for looking up something on one of the topics you want to learn more about.
Session 3
Recap
- Say out loud what was the most common mistake in R you’ve made so far.
- Open the data we worked on end of last session.
- Someone in each row must suggest a specific hypothesis test for the next row to do on that data set, cycling around. Try to make it interesting.
Loops
A for loop lets you cycle through measurements or treatments or observations, and deal with them one at a time.
The notation is: for ( counting_variable in sequence_to_count_through ) { commands based on counting_variable }
# Compare
(1:5)^2
# with
for (i in 1:5) {
print(i^2)
}
# and
for (i in 1:5) {
cat("The square of", i, "is", i^2, "\n")
}
Cycling through measurements
Let’s draw a box plot to compare treatments, but for all the measurements, one at a time.
for (measure in 8:18) {
boxplot(gluten[[measure]] ~ gluten$Treatment, col = 1:6,
ylab = names(gluten)[measure], xlab = "Treatment")
}
Generalised Linear Models
Generalised Linear Models and Mixed Linear Models use the same basis as linear models, but just have some extra extensions.
Generalised Linear Models assume a different distribution than the normal distribution for the observed values. Common examples include the Binomial distribution (0 to fixed maximum) and Negative Binomial distribution (0 to infinity).
The most commonly used GLM is called a logistic regression. It is used when the dependent variable is a random binary outcome, to predict the probability of seeing one outcome or the other. An example would be predicting whether a plant survives long enough to produce fruit or not.
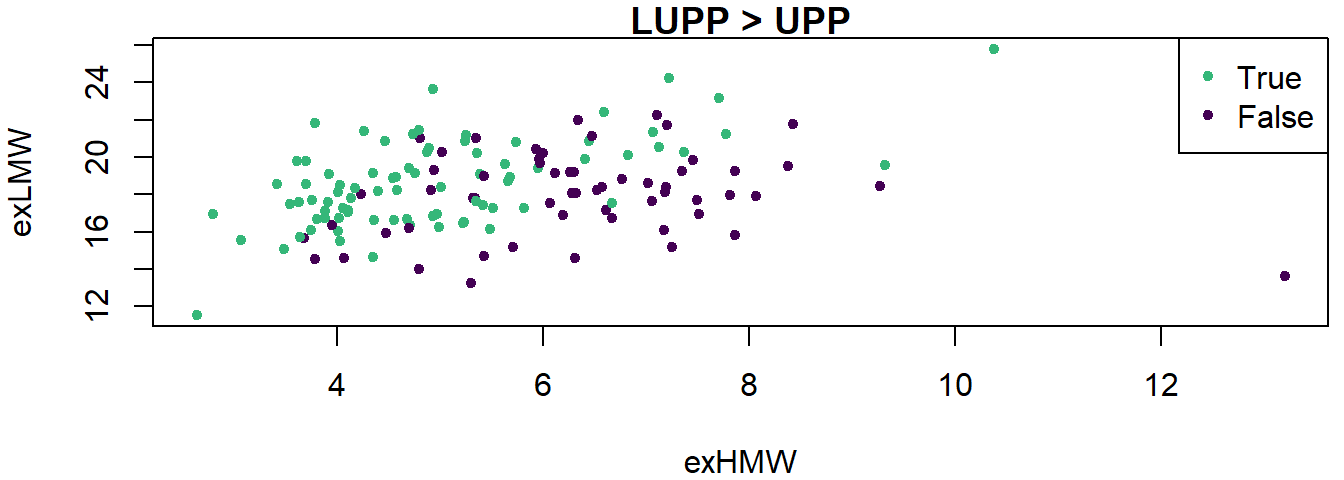
Logistic regression example
Let us try to predict whether LUPP is larger than UPP.
y <- (gluten$LUPP > gluten$UPP)
table(y)
logistic1 <- glm(y ~ exHMW + exLMW + exGLI + exAG + FP_14,
data = gluten, family = binomial())
summary(logistic1)
logistic2 <- glm(y ~ exHMW + exLMW, data = gluten, family = binomial())
summary(logistic2)
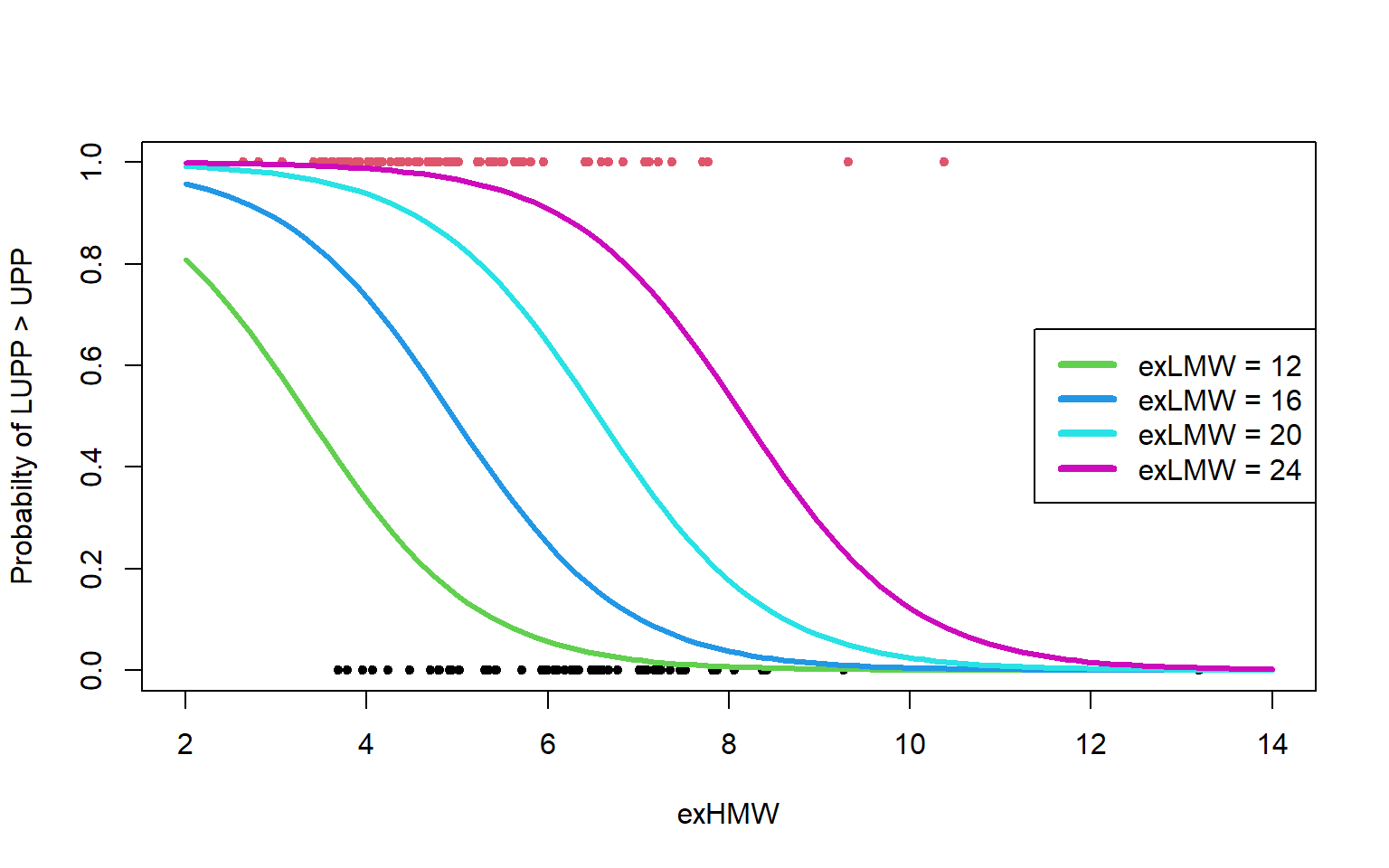
Visualise logistic regression results
- We can draw a series of plots to predict the probabilities for select values of the explanatory variables. See ?predict.glm (as opposed to ?predict.lm) for more information.
HMW <- seq(2, 14, length = 101)
par(mfrow = c(2, 2))
for (LMW in seq(12, 24, 4)) {
ypred <- predict(logistic2, newdata = data.frame(exHMW = HMW,
exLMW = rep(LMW, 101)), type = "response")
plot(HMW, ypred, type = "l", xlab = "exHMW", ylab = "Probabilty of LUPP > UPP",
main = paste("exLMW =", LMW), ylim = c(0, 1))
}

Visualise predictions
Or maybe one plot is better
HMW <- seq(2, 14, length = 101)
plot(gluten$exHMW, y, main = "", xlab = "exHMW", ylab = "Probabilty of LUPP > UPP",
col = y + 1, pch = 20, xlim = c(2, 14), ylim = c(0,
1))
for (LMW in seq(12, 24, 4)) {
ypred <- predict(logistic2, newdata = data.frame(exHMW = HMW,
exLMW = rep(LMW, 101)), type = "response")
lines(HMW, ypred, col = LMW/4, lwd = 3)
}
legend("right", paste("exLMW =", seq(12, 24, 4)), col = 3:6,
lwd = 4)
Session 3 Part 2
Mixed effects models
Sometimes experiments are done where measurements are taken repeatedly on the same subject. A subject can be a person, animal, plant, location, etc..
If there are several of them and they are a random sample of a bigger population for which you hope to do inference, then it may help to treat them as random effects.
- Suppose you take 8 soil samples from each of 10 fields.
- The soil samples within each field will be correlated to each other, so the model must include a coefficient for each field to help mitigate that.
- If you want to specifically know about those 10 fields only then just put in the fields as fixed effects (usual model, nothing new).
- But if you want to talk about fields in general then you must consider the 10 fields as a random sample of the general population of fields, in which case the fields become random effects.
Mixed model example
Let us consider the model we fitted first in Session 2, but let’s take the second measurement.
We now make the item name a random effect:
library(lme4)
summary(glutenMixed1 <- lmer(UPP ~ (1 | Name) + Treatment +
YearFactor, data = gluten))
The above model is called the random intercept model because we have a random intercept for each name.
These random intercepts are centred at zero, so if you make predictions you get predictions for an average future item of this type, not a specific one.
A more advanced option is to also have random slopes for each name based on some explanatory variable(s), but that is not applicable here.
More advanced models
For more advanced models you have a few options:
- Look for a package that addresses your specific problem. There are packages that help you with censoring, or with different data structures, or better exploration techniques, among many.
- Use extremely general purpose modelling tools like Stan. In Stan you write the model in statistical language and then ask Stan to figure out how to fit it for you (it’s got a pretty clever AI).
- Simplify your problem. Tackle one aspect of the problem at a time perhaps. It’s amazing how much you can learn and bring across simply by illustrating your data nicely.
For an example of more advanced implementations I recommend the work I did last year for Talana Cronje on opportunistic potatoes, at https://seanvdm.co.za/post/potatoes/.
If you want to learn more about Stan then check out my video presentation for StatsCon2020, at https://seanvdm.co.za/files/video/SvdMStanForStatcon2020.mp4
The catch
The big truth behind all really interesting stats is that in most cases more time was spent on working with the raw data than on the actual statistics.
Cleaning up data is the biggest and most useful skill to learn if you want to do good analysis.
A few examples can now be discussed, time permitting.
Conclusion
Thank you everyone for attending, I hope you learned things.
This is a good time to discuss general topics related to analysis of data before we end.